本文最后更新于 2021-11-06T03:52:48+08:00
某学校食堂为学生提供免费的无线网络,网络的密码是这道定积分试题的答案取前10位数字。

这道题怎么做呢?
【分析】
这是道小题(在试卷上以选择题或填空题的形式出现,不要求写出完整解答过程,只要求写出答案),被积函数很复杂,而且积分区间关于 0 对称。
这就提醒我们,可能存在捷径,要先分析被积函数每一项的奇偶性,根据奇函数在关于 0 对称的区间上的定积分为 0 的性质,化简这个函数。显然,y=x3 是奇函数,因此,含有 x3 的项,定积分都是 0。
【解】
令原式为 I,则有
I=∫−22(x3cos2x+21)4−x2dx=∫−22(x3cos2x4−x2+214−x2)dx=∫−22x3cos2x4−x2dx+∫−22214−x2dx
注意到 y=x3 是奇函数,它在区间 [−2,2] 上的定积分为 0,
所以 ∫−22x3cos2x4−x2dx=0 ,
于是 I=∫−22214−x2dx。
注意到被积函数 y=214−x2(x∈[−2,2])
恰好是椭圆 C:4x2+y2=1 的上半部分。
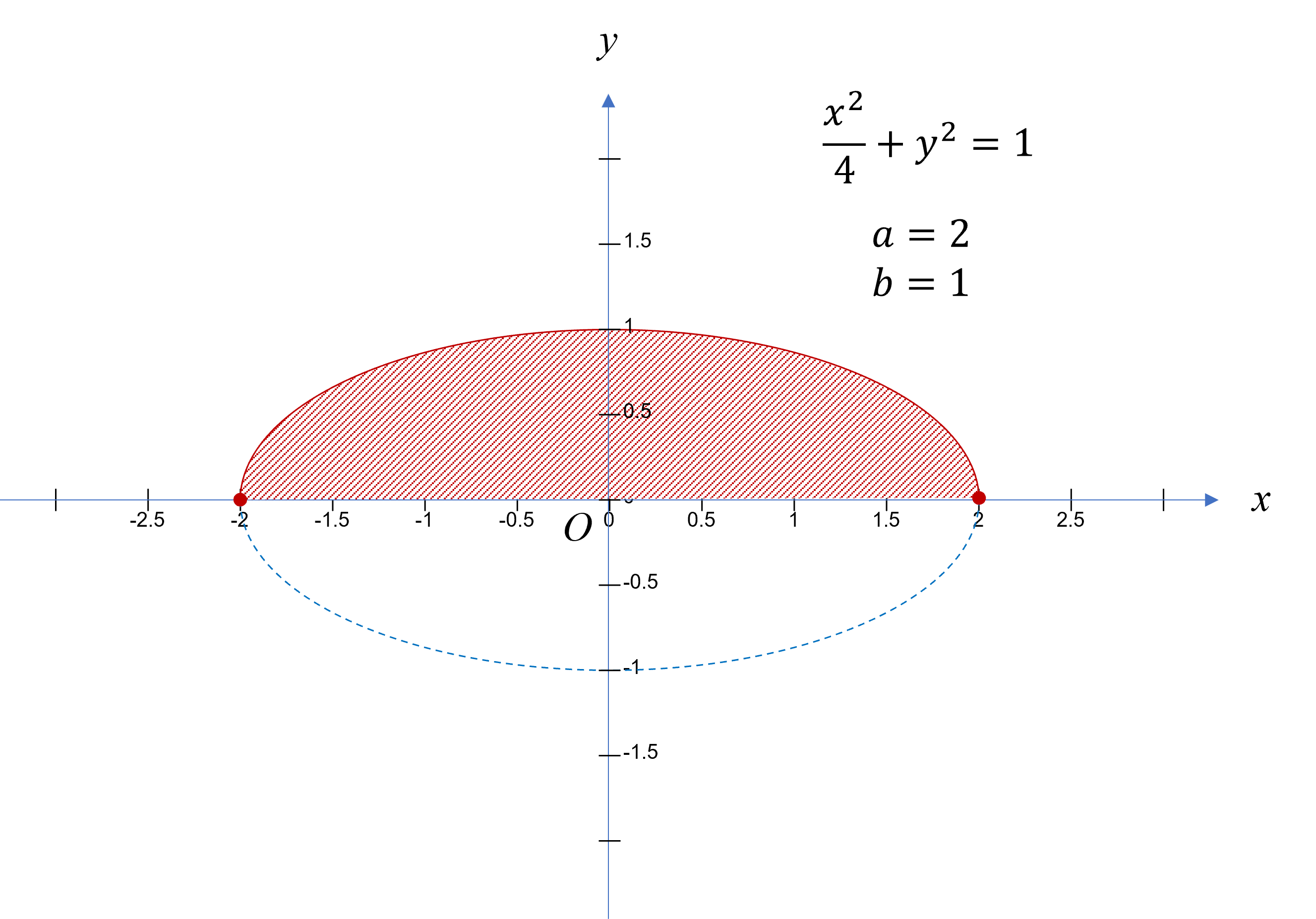
定积分 I 的几何意义是椭圆上半部分与 x 轴围成的图形的面积,
恰好是椭圆面积 SC 的一半,
所以有 I=21SC=21πab=21×π×2×1=π。
答案是 π ,所以,密码是 π 的前 10 位数字:3141592653。
【对椭圆面积公式不熟悉也没关系】
我们得到 I=∫−22214−x2dx=21∫−224−x2dx。
注意到被积函数 y=4−x2(x∈[−2,2])
恰好是圆 C:x2+y2=4 的上半部分,r=2。
定积分 ∫−224−x2dx 的几何意义是圆上半部分与 x 轴围成的图形的面积,
恰好是圆面积 SC 的一半,即 21πr2=21×π×4=2π,
所以有 I=21∫−224−x2dx=21×2π=π 。
【点评】
这种解法体现了数形结合的思想。首先,注意到积分区间关于原点对称,根据奇函数在关于 0 对称的区间上的定积分为 0 的性质化简被积函数;其次,根据定积分的几何意义,把积分问题转化成椭圆或者圆的面积问题,避免了复杂计算。
【另一种解法】
我们也可以根据牛顿—莱布尼茨公式直接计算。
∫−22(x3cos2x+21)4−x2dx=∫−22(x3cos2x4−x2+214−x2)dx=∫−22x3cos2x4−x2dx+∫−22214−x2dx=0+∫−22214−x2dx
令 x=2sint,t∈[−2π,2π],则有
∫−22214−x2dx=∫−2π2π214−4sin2t⋅2cost dt=∫−2π2π2cos2t dt=∫−2π2π(cos2t+1)dt=21(sin2t+2t)−2π2π=π
图片版权
头图:Image by Erika Varga from Pixabay



