高斯积分的求解简明笔记

高斯积分是 $\displaystyle \int_{-\infty}^{+\infty}e^{-x^2}\text{d}x$ 。

学过微积分的都知道， $\displaystyle \int e^{-x^2}\text{d}x$ 在初等函数范围内是不可积的。更何况高斯积分的积分上下界是 $+\infty$ 和 $-\infty$ 。这就决定了我们无法用微积分基本定理去求解。

但是，有数学家给出了天才的解法。如果不是吃透了定积分的定义，再加上神来之笔的灵感，是想不出这个解法的。我等后人只有膜拜了。

【解析】

令 $\displaystyle I = \int_{-\infty}^{+\infty}e^{-x^2}\text{d}x$ 。

定积分是一个数，与被积函数的自变量无关，

所以，换一下元，有 $\displaystyle I = \int_{-\infty}^{+\infty}e^{-y^2}\text{d}y$ 。

这样，凭空多出一个自变量 $y$ ，

二者相乘，得 $\displaystyle I^2 = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-(x+y)^2}\text{d}x\text{d}y$ 。

二重积分可以用极坐标换元便于求解，

令 $\displaystyle x^2+y^2=r^2, \text{d}x\text{d}y=r\text{d}r\text{d}\theta$ ，其中 $\displaystyle r\in\left[0,+\infty\right), \theta\in\left[0,2\pi\right]$ 。

有 $\displaystyle I^2 = \int_{0}^{2\pi}\int_{0}^{+\infty}e^{-r^2}r\text{d}r\text{d}\theta$

二重积分可以看做两个一元积分的乘法。既然被积函数没有 $\theta$ 这个自变量，可以把它先分离出来，

所以有 $\displaystyle I^2 = \int_{0}^{2\pi}\text{d}\theta\int_{0}^{+\infty}e^{-r^2}r\text{d}r = 2\pi\int_{0}^{+\infty}e^{-r^2}r\text{d}r$ 。

被积函数多了一个 $r$ ，就可以凑微分了，然后根据微积分基本定理求定积分，

有 $\displaystyle I^2 = -\frac{1}{2}\times 2\pi\int_{0}^{+\infty}e^{-r^2}\text{d}(-r^2) = -\pi\cdot e^{-r^2}\bigg|_0^{+\infty}=\pi$ ，

开方即得， $\displaystyle I=\sqrt{\pi}$ 。

为什么 dxdy = rdrdθ？

参考了这个知乎答案 https://www.zhihu.com/question/368888687/answer/1447917992 。

有一个假设是，同样是面积微元 $\text{d}\sigma$ ，在直角坐标系和极坐标系下是一样大小的，只是计算方式不同。

直角坐标系： $\displaystyle \text{d}\sigma=\text{d}x\text{d}y$ 。

极坐标系：

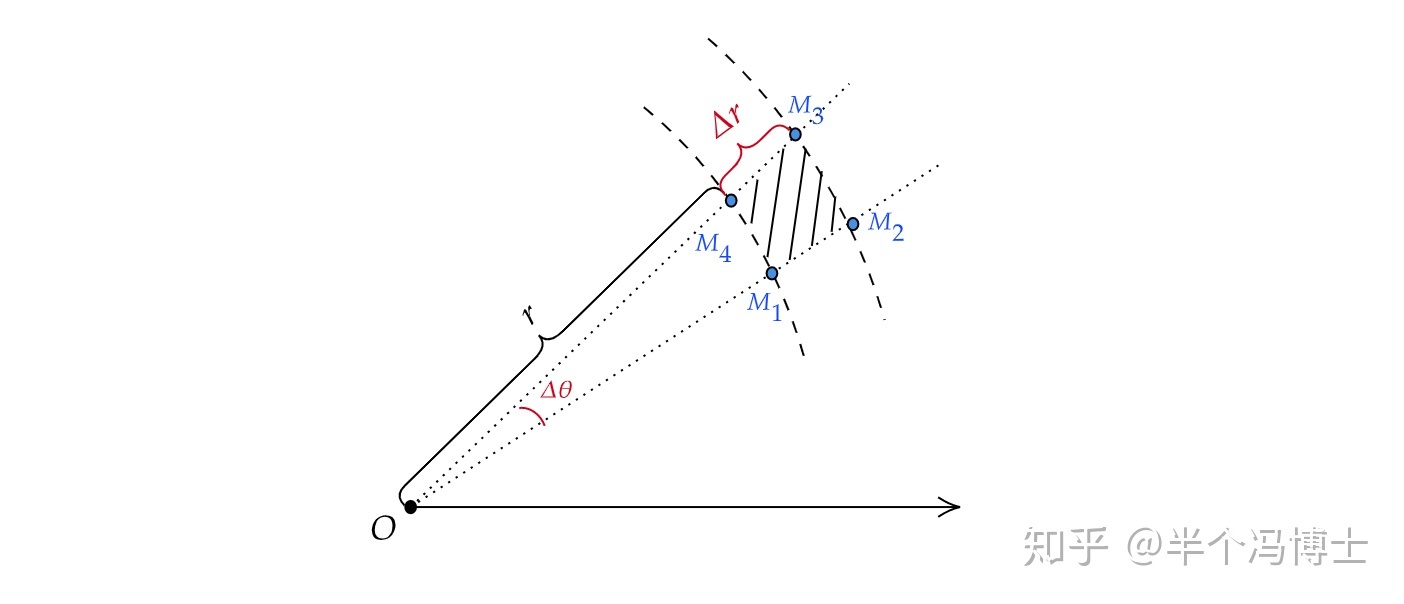
图也是原作者@半个冯博士画的

\begin{aligned} \text{d}\sigma&=S_{扇M_2OM_3}-S_{扇M_1OM_4}\\&=\frac{1}{2}\left(r+\Delta r\right)^2\cdot\Delta\theta-\frac{1}{2}r^2\cdot\Delta\theta\\&=\frac{1}{2}\left[r^2+2r\Delta r+\left(\Delta r\right)^2-r^2\right]\Delta\theta\\&=\frac{1}{2}\left[2r\Delta r+\left(\Delta r\right)^2\right]\cdot\Delta\theta \end{aligned}

由于 $\displaystyle \text{d}\theta\approx\Delta\theta$ ， $\displaystyle \left(\Delta r\right)^2$ 是 $2r\Delta r$ 的高阶无穷小（可以忽略）， $\displaystyle \text{d}r\approx\Delta r$ ，