本文最后更新于 2021-11-06T17:57:27+08:00
好多年前,谷月姐刷推特时,看到一个日本高中生贴了一道数学题求助。
【原题】
四面体 OABC において。OA⊥BC,OB⊥AC であろとする。このとき、次のことを証明せよ。
-
O から平面 ABC に下るけ垂線の足 H は。
-
OC⊥AB。
【分析】
很明显,这是一道立体几何与平面几何的综合题,把平面几何问题融入立体几何之中。它考查了线线垂直、线面垂直、三角形的垂心定理。
在中国,这样综合考查立体几何和平面几何的高中数学题比较少见。
【翻译与证明】
谷月姐在此处试翻译并证明如下。(毕竟谷月姐的日语水平还达不到用日语做数学题的地步)
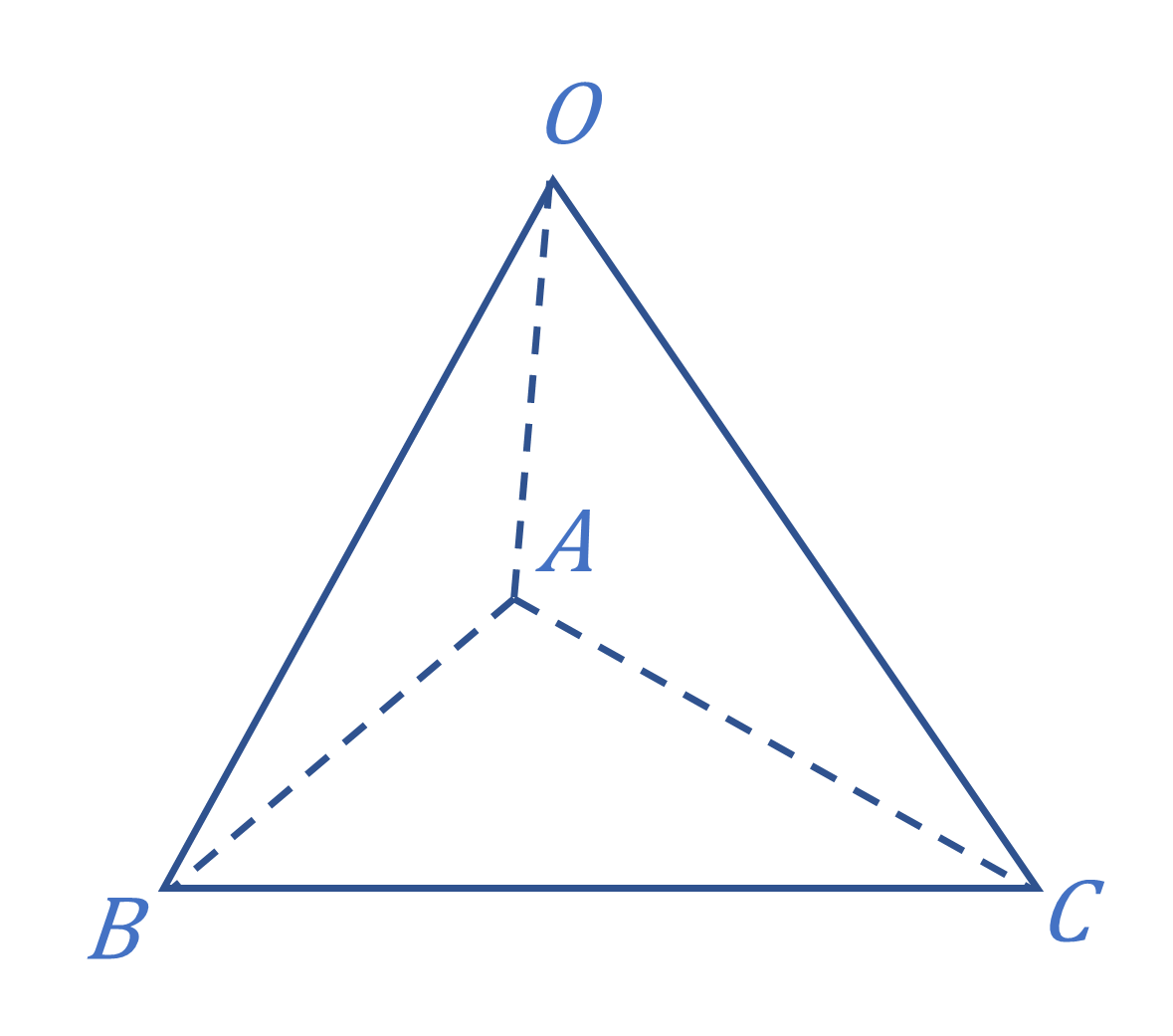
已知在四面体 OABC 中,有 OA⊥BC,OB⊥AC,证明下列命题。
- 过 O 作平面 ABC 的垂线,垂足 H 是 △ABC的垂心。
- OC⊥AB。
证法一:
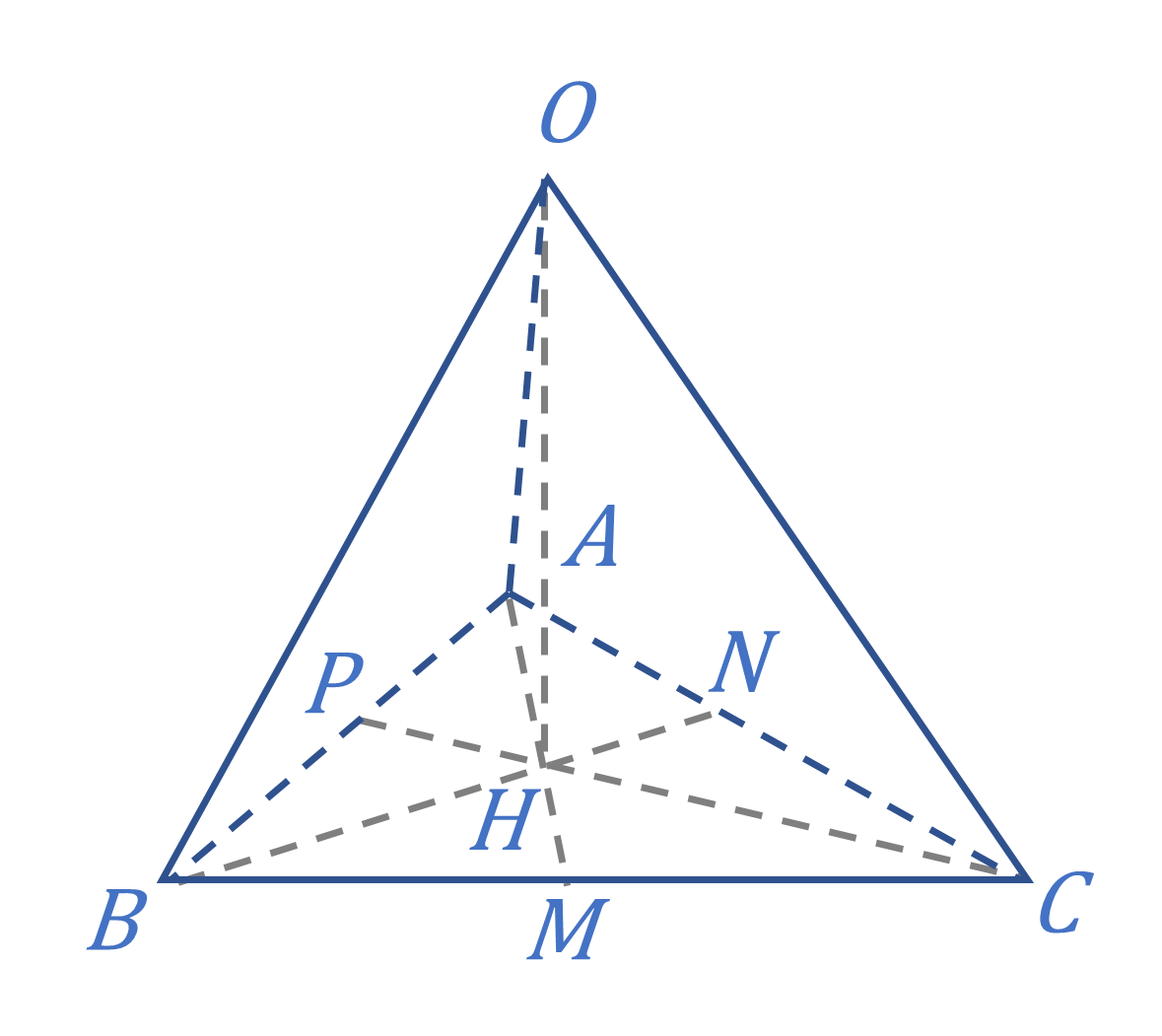
- 过 O 作 OH⊥ 平面 ABC,垂足为 H。
连结 AH 并延长,交 BC 于 M。
显然,OA 在平面 ABC 上的射影是 AM 。
∵ OA⊥BC,
∴ 由三垂线定理的逆定理可知,AM⊥BC,即 AM 是 △ABC 的高。
连结 BH 并延长,交 AC 于 N,类似地,可以证得 BN 也是 △ABC 的高。
过 C 作 CP⊥AB,
∵ AM、BN 都是 △ABC 的高,而且交于点 H,
∴ 由三角形的垂心定理可知,CP 过点 H,且 H 是 △ABC 的垂心。
- ∵ OH⊥ 平面 ABC,∴ OC 的射影是 CP。
又 ∵ CP⊥AB ,由三垂线定理可知,OC⊥AB。
证法二(不使用三垂线定理及其逆定理):
因为三垂线定理及其逆定理已经从中国高考数学考试大纲中删除,所以写一个比较麻烦的证法,说穿了就是翻来覆去利用线面垂直关系做文章。
- 过 O 作 OH⊥ 平面 ABC,垂足为 H。
连结 AH 并延长,交 BC 于 M。
∵ OH⊥ 平面 ABC,且 BC⊂ 平面 ABC,∴ OH⊥BC。
又 ∵ OA⊥BC,∴ BC⊥ 平面 OAH。
∵ AM⊂ 平面 OAH,∴ BC⊥AM,即 AM 是 △ABC 的高。
连结 BH 并延长,交 AC 于 N,类似地,可以证得 BN 也是 △ABC 的高。
过 C 作 CP⊥AB,
∵ AM、BN 都是 △ABC 的高,而且交于点 H,
∴ 由三角形垂心定理可知,CP 过点 H,且 H 是 △ABC 的垂心。
- ∵ OH⊥ 平面 ABC,且 AB⊂ 平面 ABC,∴ OH⊥AB。
又 ∵ CP⊥AB,∴ AB⊥ 平面 OCH。
又 ∵ OC⊂ 平面 OCH,∴ OC⊥AB。
证法 3:向量法
感谢知乎大佬 @大魔导师 提供。
这种证法是先证第 2 问,再证第 1 问的。
第2问:注意到恒等式 a(b−c)+c(a−b)+b(c−a)=0,
令 a=OA, b=OB, c=OC,
有 OA(OB−OC)+OC(OA−OB)+OB(OC−OA)=0。
即 OA⋅CB+OC⋅BA+OB⋅AC=0。
由题意,OA⋅CB=OB⋅AC=0,
∴ OC⋅BA=0,即 OC⊥AB。
第1问:过 O 作 OH⊥ 平面 ABC,垂足为 H,
则有 OH⊥AB、 OH⊥BC、 OH⊥AC。
连结 AH、 BH、 CH,则有:
AH⋅BC=(OH−OA)⋅BC=OH⋅BC−OA⋅BC=0
BH⋅AC=(OH−OB)⋅AC=OH⋅AC−OB⋅AC=0
CH⋅AB=(OH−OC)⋅AB=OH⋅AB−OC⋅AB=0
∴ AH⊥BC、BH⊥AC、CH⊥AC。
∴ 由三角形垂心定理可知, H 是 △ABC 的垂心。
图片版权
头图:Image by Erika Varga from Pixabay



