一道专升本模拟题难住一片大专生
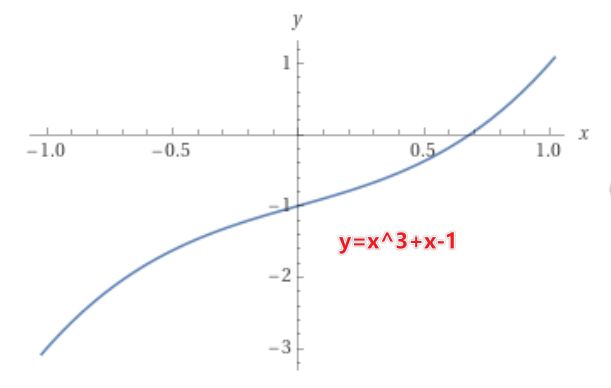
证明方程 至少有一个大于 0 的根。
其实这道题不难,但是因为高中不教反证法和零点定理,导致他们缺少了基础知识,所以他们做不出来。
这道题考查了函数与方程的思想,需要把方程的根转化为函数的零点处理。证明过程如下。
【证明】:假设方程 的所有根都小于 0。
令 ,则 ,
∴ 在定义域 上单增。
由题意, 是初等函数,在定义域上连续。
又∵ ,
∴根据零点定理,,使得 ,
即方程 有一个根 ,与假设相反。
∴假设错误,即方程 至少有一个大于 0 的根。
图片版权
题图: 用 WolframAlpha 绘制
头图:https://pixabay.com/zh/photos/munich-olympic-stadium-tv-tower-2516492/
求扫码打赏
“我这么可爱,请给我钱 o(*^ω^*)o”


一道专升本模拟题难住一片大专生
https://blog.kukmoon.com/f1152d12aa41/